ว่ากันว่าผลตอบแทนในอดีตนั้นไม่สามารถยืนยันถึงผลตอบแทนในอนาคตได้ แต่เชื่อหรือไม่ว่านั่นเป็นความจริงเพียงแค่ครึ่งเดียวจากความเชื่อในอดีตกาลเท่านั้น! ในบทความนี้เราจะมาแนะนำให้นักลงทุนทุกคนได้รู้จักกับเทคนิคการพยากรณ์แบบ Monte Carlo & Bootstrapping ซึ่งจะช่วยให้คุณสามารถประเมินถึงขอบเขตของความเป็นไปได้ของผลตอบแทนในอนาคต ภายใต้ระดับความมั่นใจทางสถิติอย่างมีหลักการ ซึ่งจะทำให้คุณสามารถคาดการณ์และวางแผนการลงทุนของคุณได้ดีขึ้นอย่างไม่น่าเชื่อกันครับ!!
เมื่อผลตอบแทนในอนาคต อาจไม่ใช่เรื่องที่ทำนายไม่ได้เสมอไป!
“Using precise numbers is, in fact, foolish; working with a range of possibilities is the better approach.”
– Warren Buffett
เรามักพบว่าในทุกวันนี้ ผลตอบแทนคาดหวังที่มาจากการวิจัยกลยุทธ์ด้วยกระบวนการ Backtest หรือแม้แต่ผลตอบแทนคาดหวังจากผลตอบแทนในอดีตของกองทุนต่างๆนั้น มักถูกนำมาใช้เป็นเครื่องมือในการโฆษณาประชาสัมพันธ์ และเป็นข้อมูลหลักที่นักลงทุนใช้ตัดสินใจว่าจะเลือกลงทุนในกองทุนกองไหนดี
อย่างไรก็ตาม เรามักจะต้องผิดหวังเมื่อพบว่าผลตอบแทนในอนาคตนั้นมักแตกต่างจากที่ได้คาดการณ์เอาไว้อยู่เสมอ ซึ่งนั่นก็เพราะ แท้ที่จริงแล้วข้อมูลในอดีตเพียงแค่บริบทเดียวนั้น ไม่อาจที่จะนำไปใช้พยากรณ์ผลตอบแทนคาดหวังหรือความเสี่ยงที่นักลงทุนต้องพบเจอในอนาคตได้ดีสักเท่าไหร่นัก
จากปัญหาที่กล่าวมานี้ ในบทความนี้เราจึงอยากจะมาแนะนำให้นักลงทุนได้รู้จักถึงกระบวนการวิเคราะห์ผลตอบแทนคาดหวัง (Expected Return) และความเสี่ยง (Worst Case Risk Scenario) จากกระบวนการ Bootstrapping ที่จะช่วยให้เราสามารถประเมินกรอบของผลตอบแทนคาดหวังได้อย่างมีเหตุมีผลดียิ่งขึ้นกันครับ
ต้นกำเนิด Monte Carlo Simulation ต้นตระกูลของกระบวนการ Bootstrapping


ภาพที่ 1 : Stanislaw Ulam (ซ้าย) นักคณิตศาสตร์ผู้บุกเบิก Monte Carlo Simulation และ John von Neumann (ขวา) ผู้ร่วมงาน วิศวกรคอมพิวเตอร์ผู้บุกเบิก Pseudorandom Number Generator
ก่อนที่เราจะเข้าสู่รายละเอียดการของกระบวนการ Bootstrapping กันนั้น เราจะมาย้อนดูประวัติความเป็นมาและเหตุผลที่ต้องมีการพัฒนากระบวนการนี้ขึ้นมากันซักนิด โดยเมื่อย้อนกลับไปในช่วงสงครามโลกครั้งที่ 2 ที่ศูนย์วิจัย Los Alamos (สถานที่พัฒนาโครงการ Manhattan Project ที่สร้างระเบิดนิวเคลียร์ลูกแรกของโลก)
ในขณะนั้น ทางศูนย์วิจัยกำลังทำโครงการวิจัยวัสดุที่จะนำมาสร้างเป็นเกราะกั้นรังสี ซึ่งมีความจำเป็นต้องทำการทดลองหาระยะทางเฉลี่ยที่นิวตรอนจะสามารถเดินทางทะลุวัสดุชนิดต่างๆได้ แต่เนื่องจากปัจจัยสุ่มที่เกิดขึ้นในการทดลอง ถึงแม้จะมีข้อมูลที่ต้องการทั้งหมดนักวิทยาศาสตร์ก็ยังไม่สามารถไขปัญหาด้วย Deterministic Model แบบเดิมซึ่งเป็นวิธีการคำนวณที่จำเป็นต้องรู้ค่าตัวแปรทั้งหมดได้
จากปัญหาที่เกิดขึ้น Stanislaw Ulam นักคณิตศาสตร์และนิวเคลียร์ฟิสิกส์ จึงได้มีความพยายามที่จะแก้ปัญหานี้โดยการเสนอการแก้ปัญหาด้วยแนวทางการทดลองแบบสุ่ม (Random Experiment) โดยได้แรงบันดาลใจตอนที่เค้าป่วยอยู่บนเตียงและพยายามที่จะหาโอกาสความน่าจะเป็น (Probability) ที่จะชนะเกมไพ่ Solitare โดยในที่สุดเค้าได้แนวคิดในการแก้ปัญหาด้วยการทำการทดลองเล่น Solitare ซ้ำๆจำนวนหลายๆครั้งแล้วนับจำนวนครั้งที่ชนะ แทนที่จะต้องคำนวนความน่าจะเป็นออกมาด้วยสูตรคณิตศาสตร์
เรื่องที่น่าสนใจก็คือ ตอนนั้นโครงการการทดลองในศูนย์วิจัย Los Alamos ทั้งหมดนั้นเป็นความลับทางทหาร ทำให้โครงการนี้ถูกตั้งชื่อรหัสว่า Monte Carlo โดยตั้งตามลุงของ Ulam ที่ชอบยืมเงินญาติๆไปเล่นการพนันที่คาสิโน Monte Carlo ในประเทศ Monaco ซึ่งในภายหลังโครงการวิจัยนี้กลับมีคุณูปการต่อความก้าวหน้าทางสถิติและวิทยาศาสตร์เป็นอย่างมาก จนได้กลายมาเป็นแนวทางต้นแบบของ Monte Carlo Simulation ที่เรารู้จักกันในปัจจุบันนั่นเองครับ
อย่างไรก็ตาม กระบวนการสร้างตัวเลขสุ่มยังเป็นกระบวนการที่ยังต้องใช้เวลามาก จนเป็นที่มาให้ John von Neumann วิศวกรคอมพิวเตอร์ ได้ทำการบุกเบิกสูตรคณิตศาสตร์ที่ใช้ในการสร้างตัวเลขสุ่มในคอมพิวเตอร์หรือ Pseudo Random Number ขึ้นมา (ซึ่งถือเป็นต้นตระกูลของสูตรที่ใช้สร้างตัวเลขสุ่มในโปรแกรมวิเคราะห์สถิติที่ใช้กันอยู่ทั่วไปทุกวันนี้) โดย Program จะทำงานผ่านเครื่องคอมพิวเตอร์ยุคแรกที่เรียกกันว่า “ENIAC” ซึ่งเป็นชื่อย่อมาจาก Electronic Numerical Integrator And Computer ซึ่งถือได้ว่าเป็นอภิมหาโปรเจคโครงการหนึ่งในสมัยนั้นเลยทีเดียว
จากความสำเร็จในครั้งนั้นเป็นต้นมา ประกอบกับการเพิ่มขึ้นของพลังการประมวลผลของ Computer ทำให้ Monte Carlo Simulation ได้ถูกนำมาใช้ในการสร้าง Model และจำลองปรากฏการณ์ทางวิทยาศาสตร์มากมายทั้งในสาขาฟิสิกส์, เคมี, การเงิน รวมถึงแก้สมการคณิตศาสตร์ต่างๆที่เกี่ยวข้องกับตัวแปรสุ่ม (Random Variable) อย่างกว้างขวาง จนทำให้เกิดความก้าวหน้าขององค์ความรู้ในวงการวิชาการสาขาต่างๆเป็นอย่างมากจวบจนถึงปัจจุบัน

ภาพที่ 2 : “ENIAC” หนึ่งในเครื่อง Computer ยุคแรก
จาก Monte Carlo สู่ Bootstrapping Simulation ในแวดวงการลงทุน

ภาพที่ 3 : Bradley Efron นักสถิติชาวอเมริกันผู้คิดค้นกระบวนการ Bootstrapping
หลังจากที่ได้รู้ถึงต้นกำเนิดของกระบวนการ Monte Carlo Simulation คร่าวๆกันไปแล้วนั้น เรื่องถัดมาที่คุณควรรู้ก็คือต้นกำเนิด, เหตุผล และการพัฒนาต่อยอดจนเป็นที่มาของกระบวนการแบบ Bootstrapping Simulation กันครับ
โดยเหตุผลหลักๆที่การใช้เทคนิค Monte Carlo Simulation แบบดั้งเดิมนั้นไม่เพียงพอที่จะตอบโจทย์การวิเคราะห์และคาดการณ์ข้อมูลผลตอบแทนในอนาคตในตลาดหุ้นนั้นก็คือ Monte Carlo Simulation จะทำการสุ่มตัวอย่างจากรูปแบบการกระจายตัวของข้อมูลแบบปกติ (Normal Distribution) ที่สร้างขึ้นมาจากค่า Mean และ Standard Deviation ของกลุ่มตัวอย่าง ซึ่งอาจจะทำให้เกิดความไม่สมจริงขึ้นทันทีถ้าผลตอบแทนนั้นไม่ได้มีการกระจายตัวแบบปกติเช่นกัน
แน่นอนว่า ลักษณะของข้อมูลแบบนี้ถือว่าเป็นเรื่องปกติของข้อมูลที่เกิดขึ้นจากตลาดหุ้น นอกจากนั้นแล้ว ปัจจัยข่าวสารนับไม่ถ้วนในทุกๆวันมักทำให้เกิดความแปรปรวนและสับสนในการตัดสินใจของนักลงทุนอยู่ตลอดเวลา (Noise) โดยปรากฏการณ์เหล่านี้ทำให้เกิดทั้งค่า Outlier และการกระจายตัวของข้อมูลแบบสุ่มที่ไม่อยู่ในรูปแบบทางทฤษฎีใดสักเท่าไหร่นัก
ดังนั้นแล้วเมื่อเป้าหมายของเราคือความต้องการที่จะหาความน่าจะเป็นของผลตอบแทนและความเสี่ยงของผลตอบแทน ที่อาจเกิดขึ้นอนาคตในสภาวะตลาดที่เต็มไปด้วย ”ตัวแปรสุ่ม” นั้น กระบวนการ Bootstrapping Simulation ซึ่งอาศัยเพียงกลุ่มตัวอย่างที่มีความน่าเชื่อถือในอดีต (Representative Sample) จึงกลายเป็นเครื่องมือที่นิยมถูกนำมาใช้เพื่อการประมาณการณ์ Performance ของราคาหุ้น, มูลค่ากองทุน หรือประสิทธิภาพต่างๆของผล Backtest ที่อาจเกิดขึ้นมาในอนาคต
สรุปโดยย่อแล้วก็คือ Bootstrapping เป็นหนึ่งในเทคนิคการสุ่มตัวอย่าง (Resampling) ที่ต่อยอดมาจาก Monte Carlo Simulation กัน โดยมันได้ถูกตีพิมพ์เผยแพร่เป็นครั้งแรกโดย Bradley Efron นักสถิติชาวอเมริกัน เมื่อปี 1979 นั่นเองครับ
กระบวนการ Bootstrapping แบบนาทีเดียวรู้เรื่อง!
เพื่อที่จะให้เพื่อนๆนักลงทุนได้เห็นภาพกันอย่างชัดเจนและเข้าใจได้ง่ายที่สุดนั้น ในบทความนี้เราจะขอไม่พูดถึงที่มาที่ไปในทางทฤษฎีหรือสูตรคณิตศาสตร์ต่างๆให้ปวดหัวเกินไป แต่เราจะมาทำการทดลองสาธิตขั้นตอนและวิธีการทำงานของกระบวนการสุ่มตัวอย่างที่เรียกว่ากันว่า Bootstrapping กันครับ
โดยจุดเด่นของกระบวนการ Bootstrapping นั้น จะช่วยทำให้เราสามารถสร้างชุดข้อมูลใหม่ขึ้นมาจากชุดข้อมูลเดิมที่มีอยู่ด้วยวิธีการเลือกสุ่มแบบคืนที่ (Sampling with Replacement) โดยในการอธิบายให้เห็นภาพง่ายที่สุดนั้น เราอยากให้คุณลองจินตนาการถึงลูกกวาดหลากสีในโหลแก้วตามภาพด้านล่างกันครับ

ภาพที่ 4 : จินตนาการว่าลูกกวาดในโหลคือชุดข้อมูลที่จะถูกนำมา Bootstrap
ทุกครั้งที่มีการหยิบลูกกวาดออกมา ให้เราทำการบันทึกสีของลูกกวาดที่หยิบได้แล้วเอาลูกกวาดใส่โหลแก้วกลับคืนเข้าไป ซึ่งจะทำให้มีโอกาสความน่าจะเป็นที่จะหยิบลูกกวาดสีเดิมนั้นยังคงเดิม (เพราะเราไม่ได้แยกลูกกวาดที่เราหยิบไปแล้วออกมาจากโหล) โดยเราจะทำการหยิบลูกกวาดและบันทึกข้อมูลสีไปเรื่อยๆจนกว่าจะครบตามจำนวนลูกกวาดที่เราต้องการ จึงจะถือว่าเป็นการสิ้นสุด 1 รอบ (Iteration) ของการสุ่มชุดข้อมูล
ซึ่งเมื่อทำกระบวนการนี้ซ้ำๆกันในจำนวน iteration ที่มากพอ (มากกว่า 1,000 iteration ขึ้นไป) ตามทฤษฎีแล้วจะทำให้เราสามารถมองเห็นขอบเขตของการกระจายตัว (Distribution) ของกลุ่มชุดข้อมูลใหม่ จนช่วยให้เราสามารถคำนวณถึงคุณลักษณะต่างๆทางสถิติของกลุ่มประชากรได้อย่างน่าเชื่อถือมากขึ้นนั่นเอง
ซึ่งเมื่อมองในบริบทของการประเมินผลตอบแทนและความเสี่ยงในการลงทุนแล้ว มันก็คือการกระจายตัวของเส้นการเติบโตของเงินทุน (Equity Curve) จนช่วยให้เราสามารถอนุมาน ค่า Performance Statistic หรือสถิติต่างๆในการลงทุนออกมาได้นั่นเอง
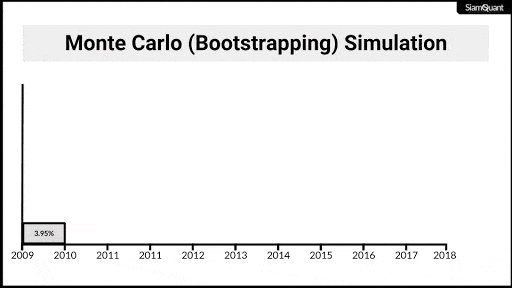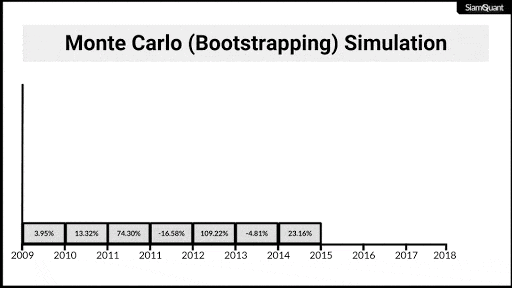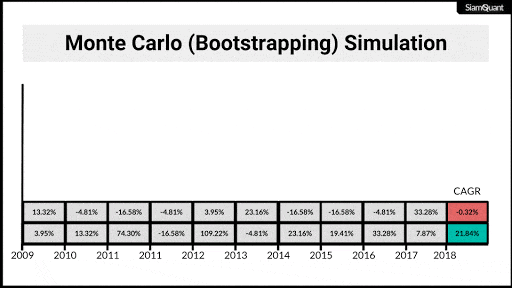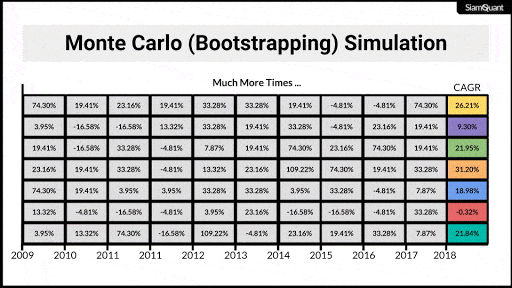
ภาพที่ 5 : ภาพเคลื่อนไหวแสดงตัวอย่างการ Bootstrapping ผลตอบแทนรายปี เพื่อนำไปคำนวณผลตอบแทนทบต้น (CAGR) เพื่อนำไปทำการอนุมานทางสถิติต่อไป
ประโยชน์ของการวิเคราะห์ด้วยเทคนิค Bootstrapping
- จุดเด่นของกระบวนการ Bootstrapping คือความสามารถคาดการณ์ความน่าจะเป็นของค่าสถิติในระดับความมั่นใจต่างๆ จากข้อมูลที่มี Noise สูงได้แม่นยำกว่าวิธีการอื่นที่ใช้การสุ่มจากสมมุติฐานการกระจายแบบปกติ (Assumption of Normality)
- การนำกระบวนการ Bootstrapping มา Resampling ผลลัพธ์ที่ออกมาจากกระบวนการ Backtest เป็นการวิเคราะห์ค่าสถิติในมิติของความน่าจะเป็น (Pprobability) ซึ่งเป็นการให้ความสำคัญกับระบบที่มีความสามารถในการทำกำไรในระยะยาวอย่างยั่งยืนมากกว่าระบบที่ได้กำไรจากแค่บาง Trade (Windfall profit) หรือแค่บางช่วงเวลา
- ทำให้นักลงทุนได้รู้ถึงผลกำไรคาดหวัง (Expected Return) ที่ควรจะเป็นของระบบโดยลดปัญหาของการโดนโฆษณาชวนเชื่อจากผล Backtest ที่อาจทำให้เกิดการคาดหวังผลตอบแทนที่สูงเกินจริง (Over-Expectation of Return) และประเมินความเสี่ยงต่ำกว่าความจริง (Under-Expectation of Risk)
- ทำให้นักลงทุนสามารถที่จะประเมินความเสี่ยงแบบ Worst Case ที่เหมาะสมกับตัวเองได้ก่อนเริ่มลงทุนจริงซึ่งจะมีผลอย่างมากต่อจิตวิทยาการลงทุน
ขีดจำกัดของการวิเคราะห์ด้วยเทคนิค Bootstrapping
- กลุ่มตัวอย่างเริ่มต้น (Sample) ต้องเป็นตัวแทนที่น่าเชื่อถือ (Representative) ดังนั้น หากเรานำผลตอบแทนที่ได้จากการ Backtest ที่ Overfit หรือเกินจริงมา ค่าที่ได้ก็จะไม่น่าเชื่อถือเช่นกัน
- นักลงทุนแต่ละคนนั้นจะต้องเป็นผู้เลือกที่จะเชื่อค่าสถิติในระดับความมั่นใจ (Confidence Level) ที่เหมาะสมกับตนเอง
- ถ้าจำนวน Observation ที่น้อยในข้อมูลดิบ (เช่นในกรณีที่ข้อมูลผลตอบแทนนั้นมีจำกัดแค่ในช่วงระยะเวลาที่สั้น) การ resampling ด้วยเทคนิค Bootstrapping อาจไม่สามารถทำให้เราเห็นการกระจายตัวของค่าสถิติ (distribution) ที่แท้จริงได้
- โดยทั่วไปแล้วต้องทำการ Bootstrapping มากกว่า 1,000 iteration ขึ้นไปถึงจะสามารถเชื่อถือค่าประมาณการสถิติที่ออกมาได้ซึ่งทำให้อาจต้องใช้เวลาและทรัพยากร Computer ที่มากขึ้นในการทำการวิจัย
มาลองประเมินผลตอบแทนของดัชนี SET TRI ด้วยเทคนิค Bootstrapping กัน!

ภาพที่ 6 : เส้น Cumulative Return ของดัชนี SET TRI (ข้อมูลตั้งต้น)
สำหรับตัวอย่างของการประยุกต์ใช้เทคนิคการวิเคราะห์ผลตอบแทนและความเสี่ยงจาก Bootstrapping นั้น เพื่อหลีกเลี่ยงผลกระทบที่อาจเกิดขึ้นกับทางทีมงานและผู้อื่นนั้น ในบทความนี้เราจึงขออนุญาติที่จะไม่นำเอาผลตอบแทนของกองทุนต่างๆหรือ Algo บางอย่างมาสาธิตให้เห็นกัน (กลัวโดนฟ้องครับ 😀 )
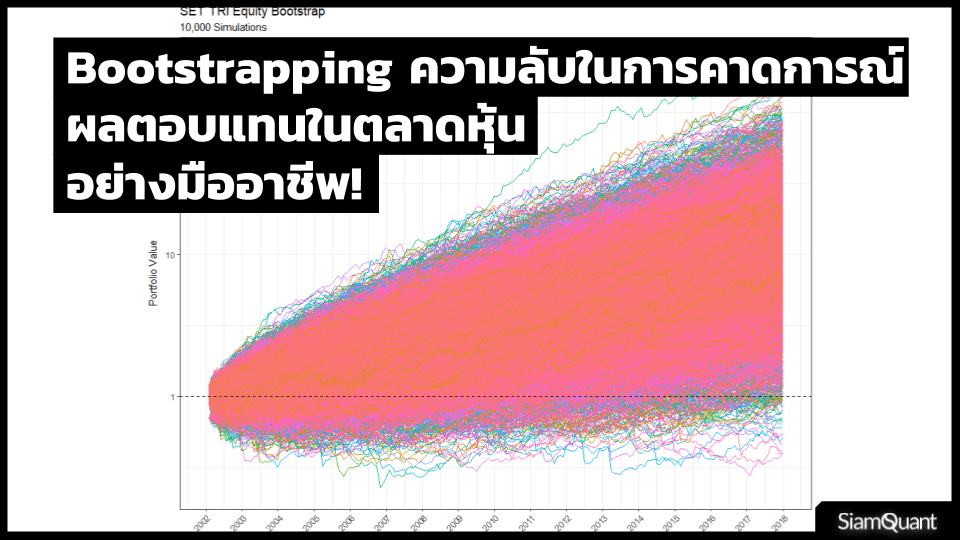
แต่ในบทความนี้ เราจะนำเอาผลตอบแทนรายเดือนแบบ Monthly Return ของดัชนี SET TRI ซึ่งถือเป็นตัวแทนผลตอบแทนของตลาดหุ้นไทยแบบรวมปันผลเข้าไปด้วย (และยังเป็นตัวแทนของ Passive Fund ส่วนใหญ่) มาทำการ Simulation เพื่อประมาณการณ์ผลตอบแทนในอนาคตกัน โดยจะทำการรวมข้อมูลผลตอบแทนรายเดือนให้เป็นกลุ่ม กลุ่มละ 3 เดือน เพื่อดำรงความสัมพันธ์ในการเคลื่อนไหวของแนวโน้มราคาเอาไว้ (ไม่อย่างนั้นจะกลายเป็นว่าผลตอบแทนในแต่ละเดือนจะไม่มีความสัมพันธ์กันเลย) และจะ Simulation โดยอาศัยข้อมูลตั้งแต่ต้นปี 2002 ถึงปลายปี 2017 ซึ่งจะทำการสุ่มซ้ำเป็นจำนวน 10,000 รอบ (Iteration) เพื่อให้เกิดจำนวนการกระจายตัวของข้อมูลที่เพียงพอจะทำการอนุมานผลทางสถิติกันออกมา โดยได้ผลลัพท์ออกมาเป็นดังภาพที่ 7 ด้านล่างนี้

ภาพที่ 7 : กลุ่มของเส้น Equity Curve (Cumulative Return) ของดัชนี SET TRI เริ่มต้นที่ค่า 1 เท่า หลังจากทำการ Bootstrapping เป็นเวลา 16 ปี จำนวน 10,000 ครั้ง
โดยเราจะเห็นได้ว่า จากผลตอบแทนรายเดือนส้นเดียว (บริบทเดียวในอดีต) ของดัชนี้ SET TRI นั้น เมื่อมันได้ผ่านกระบวนการ Bootstrapping ออกมานั้น มันได้แสดงให้เราเห็นได้ถึงความเป็นไปได้นับ 10,000 รูปแบบของผลตอบแทน ซึ่งเกิดขึ้นทั้งในแง่บวกและแง่ลบ (มีโอกาสทั้งกำไรและขาดทุนในระยะยาว)
โดยเมื่อนำเส้น Equity Curve (Cumulative Return) แต่ละเส้นที่ได้มาทำการคำนวณค่าเฉลี่ยผลตอบแทนทบต้นหรือ CAGR ออกมา และนำมาสร้างตารางแจกแจงความถี่ต่อนั้น เราจะสามารถมองเห็นขอบเขตการกระจายตัวของผลตอบแทนของ SET TRI ได้ตามภาพที่ 8

ภาพที่ 8 : การกระจายตัวของค่า CAGR จากกลุ่มเส้น Equity Curve ของดัชนี SET TRI ที่ผ่านการ Bootstrapping ในภาพที่ 7
โดยการกระจายตัวของค่า CAGR ในภาพที่ 8 นั้น นอกจากจะสามารถนำไปทำการยืนยันความมีนัยยะสำคัญทางสถิติกับจุดอ้างอิงบางอย่าง เช่น Hypothesis Testing ว่าการกระจายตัวของผลตอบแทนอยู่เหนือ 0 อย่างมีนัยยะสำคัญทางสถิติหรือไม่ (หรือพูดง่ายๆว่าเกิดขึ้นด้วยความบังเอิญมากแค่ไหน) มันยังสามารถที่จะถูกนำมาเรียบเรียงใหม่ในรูปแบบชาร์ต Cumulative Distribution Function หรือ CDF เพื่อทำการประมาณการณ์ถึงผลตอบแทนในอนาคตตามระดับความน่าจะเป็นต่อไป โดยภาพที่ 9 นั้น ได้แสดงให้เห็นถึงข้อมูลการกระจายตัวของความน่าจะเป็น (Probability) โดยค่าในแกนตั้งคือความน่าจะเป็นที่ 0 ถึง 100%

ภาพที่ 9 : ชาร์ต CDF (Cummulative Distribution Function) ที่แสดงข้อมูลการกระจายตัวของความน่าจะเป็น (probability) ของค่า CAGR จากภาพที่ 8
| Confidence Level | CAGR (%) | Max Drawdown (%) |
| 1% | 28.15 | -24.91 |
| 5% | 23.80 | -31.37 |
| 10% | 21.38 | -35.37 |
| 25% | 17.37 | -45.66 |
| 50% | 12.90 | -59.06 |
| 75% | 8.30 | -73.63 |
| 90% | 4.26 | -83.45 |
| 95% | 1.71 | -87.36 |
| 99% | -2.86 | -93.23 |
ตารางที่ 1 : ตารางสรุปผลตอบแทนคาดหวัง (CAGR) และความเสี่ยง (Max Drawdown) ในระดับความมั่นใจต่างๆ ของดัชนี SET TRI จากกระบวนการ Bootstrapping ผลตอบแทนรายเดือนจำนวน 10,000 ครั้ง
โดยที่ชาร์ตและตาราง CDF ในด้านบนนี้เอง ที่ทำให้เราสามารถประเมินค่าผลตอบแทนทบต้นคาดหวัง (Expected CAGR) ที่เราอาจจะได้รับจากการลงทุนในตลาดหุ้นไทยแบบรวมปันผล (ดัชนี SET TRI) ภายใต้ระดับความน่าจะเป็นต่างๆได้! โดยที่ระดับความมั่นใจ (Confidence Level) ตามมาตราฐานในการประเมิน Worst Case Scenario ในทางสถิติโดยทั่วไปนั้น จะอยู่ที่ระดับ 95% ถึง 99% นั่นเองครับ!!
มันจึงทำให้เราสามารถประเมินผลออกมาได้อย่างง่ายๆว่า ผลตอบแทนในระยะยาวของตลาดหุ้นไทยแบบรวมปันผลในอนาคต (ซึ่งถือเป็นตัวแทนของกองทุนรวมแบบ Passive Fund ส่วนใหญ่) โดยอ้างอิงจากกลุ่มข้อมูลผลตอบแทนในอดีตนั้นพบว่า มีโอกาสให้ผลตอบแทนทบต้น CAGR ไม่น่าจะต่ำกว่า 1.71% และมีการถดถอยของมูลค่าจากจุดสูงสุดหรือ Maximum Drawdown อยู่ไม่น่าจะเกินกว่า -87.36% ด้วยระดับความมั่นใจที่ 95% ตามข้อมูลที่เกิดขึ้นจากการ Simulation นี่จึงควรเป็นระดับผลตอบแทนและความเสี่ยงที่คุณควรเผื่อใจเอาไว้หากเกิดสถานการณ์ที่เลวร้ายในอนาคตขึ้นนั่นเอง
รู้ไปแล้วจะได้อะไร!?
จะเห็นได้ว่า จากผลการทดลองการนำดัชนี SET TRI มาทำการ Bootstrapping เพื่อประเมิณผลตอบแทนเป็นช่วงระยะนั้น (Range Estimation) มีความแตกต่างแตกต่างจากการประเมิณผลตอบแทนในอนาคตด้วยวิธีการคิดจากค่าเฉลี่ยผลตอบแทนในอดีตเพียงอย่างเดียวเป็นอย่างมาก (Point Estimation)
ซึ่งด้วยความที่อนาคตนั้นเป็นสิ่งที่ไม่เคยจะแน่นอน โดยมันอาจจะดีหรือร้ายมากขึ้นก็ได้ มิหนำซ้ำแล้ว เหตุการณ์ดีร้ายต่างๆอาจเกิดขึ้นติดๆกันหรือไม่เกิดขึ้นสักเท่าไหร่ก็ได้เช่นกัน ดังนั้น การตั้งคำถามที่ว่า “อะไรจะเกิดขึ้น หากอนาคตนั้นไม่เหมือนเดิม?” เช่นนี้ จึงมีประโยชน์มากในการประเมินถึงกรอบของผลตอบแทนและความเสี่ยงที่อาจจะเกิดขึ้นในอนาคต และยังช่วยควบคุมจิตวิทยาในการลงทุนของเราให้มีเหตุมีผลยิ่งขึ้นได้อีกด้วย
โดยหากสังเกตให้ดีจะพบว่า ผลตอบแทน CAGR ที่ประเมิณได้จากระดับความมั่นใจที่ 95% นั้น ย่ำแย่ลงกว่าที่ระดับราว 50% ถึงราวๆ 10% ต่อปีเลยทีเดียว ซึ่งหากเราเข้าใจและได้เตรียมการรับมือทางการเงินในกรณีที่เลวร้ายไว้ก่อน ก็จะช่วยผ่อนทุเลาความเสียหายในการลงทุนลงนั่นเอง
และนี่ก็คือเนื้อหาโดยสังเขปของการคาดการณ์ผลตอบแทนด้วยเทคนิค Bootstrapping ที่พวกเราหวังว่าจะมีประโยชน์กับนักลงทุนทุกท่าน ขอบคุณที่อ่านกันมาจนจบ แล้วพบกันใหม่ในบทความหน้าครับ! 😀
| SET TRI | Past Performance | Bootstrapping 95% CL |
| Cumulative Profit (Start @1) | 8.52 | 1.32 |
| Annualized Return (%) | 15.21 | 1.71 |
| Annualized Standard Deviation | 19.97 | 24.55 |
| Annualized Sharpe (Rf = 4%) | 0.74 | 0.08 |
| Maximum Drawdown (%) | -53.66 | -87.36 |
ตารางที่ 2 : ตารางเปรียบเทียบค่าสถิติต่างๆที่อาจเกิดขึ้นในอนาคต โดยคำนวณจากผลตอบแทนในอดีตของ SET TRI บริบทเดียว (Single Point Esitimation) และค่าสถิติที่เกิดขึ้น ณ ระดับความมั่นใจ 95 % จากกระบวนการ Bootstrapping (Range Estimation)
References :
Monte Carlo Method : https://en.wikipedia.org/wiki/Monte_Carlo_method
Bootstrapping : https://en.wikipedia.org/wiki/Bootstrapping_(statistics)