เพื่อนๆพี่น้องๆนักลงทุนคงทราบกันดีว่า “กำไร” ที่เราได้รับจากการลงทุนในตลาดหุ้นนั้นไม่ได้เกิดขึ้นมาจากสาเหตุเพียงสาเหตุเดียว ยกตัวอย่างเช่น เราอาจจะได้กำไรจากการที่เราเลือกซื้อหุ้นได้ถูกจังหวะจากการวิเคราะห์ด้วยปัจจัยเทคนิค, จากการซื้อหุ้นเมื่อราคาอยู่ต่ำกว่ามูลค่าเหมาะสม, จากการเก็งกำไรจากข่าวลือของการควบรวมกิจการ หรือแม้แต่แค่เพียงเพราะตลาดปรับตัวขึ้นเฉยๆ
ซึ่งในกรณีที่เราต้องการวิเคราะห์ประสิทธิภาพของกลยุทธ์ที่เราเลือกใช้ เราจะพบกับปัญหาในการไม่สามารถแยกแยะได้ว่าปัจจัยไหนกันแน่ที่เป็นตัวขับเคลื่อนผลตอบแทนของพอร์ตโฟลิโอหรือจริงๆแล้วความสำเร็จทั้งหมดนั้นเกิดขึ้นมาจากเพียงแค่ความบังเอิญ!!
โดยเฉพาะอย่างยิ่งกับนักลงทุนที่เลือกลงทุนในกองทุนแบบ Active Fund ที่มีค่าบริหารจัดการสูงกว่ากองทุนแบบ Passive Fund อยู่ค่อนข้างมาก เพราะเราต้องการรู้ว่าค่าบริหารจัดการที่เราจ่ายไปนั้นคุ้มค่ากับสิ่งที่เราได้รับหรือไม่
ซึ่งในบทความนี้ ผมจะมาแนะนำให้เพื่อนๆได้รู้จักกับเทคนิคการวิเคราะห์ “Return Based Style Analysis” โดยเป็นหนึ่งในวิธีการวิเคราะห์ปัจจัยที่ขับเคลื่อนผลตอบแทนของการลงทุน ด้วยวิธีการทางสถิติ ซึ่งจะเข้ามาช่วยในการแก้ปัญหาเหล่านี้กันครับ
ประวัติความเป็นมาของ Return Based Style Analysis
ก่อนที่เราจะเข้าไปถึงรายละเอียดเทคนิคการวิเคราะห์ “Return Based Style Analysis” ผมจะขอเล่าเกริ่นถึงประวัติความเป็นมาของมันกันซักนิด โดยแนวคิดนี้ถูกตีพิมพ์ในวารสารทางวิชาการในปี 1989 โดย William F. Sharpe นักเศรษฐศาสตร์รางวัลโนเบลชื่อดัง ผู้มีผลงานที่มีคุณประโยชน์ต่อแวดวงการเงินและการลงทุนหลายชิ้นยกตัวอย่างเช่น การเป็นหนึ่งในผู้ร่วมพัฒนา Capital Asset Pricing Model (CAPM) ทฤษฎีที่เป็นรากฐานของการบริหารพอร์ตโฟลิโอที่ยังคงใช้อยู่ในปัจจุบัน, การคิดค้นมาตราวัดผลตอบแทนต่อความเสี่ยง Sharpe Ratio ที่ทุกคนคงคุ้นเคยกันเป็นอย่างดีเป็นต้น

ภาพที่ 1: Prof. William F. Sharpe นักเศรษฐศาสตร์รางวัลโนเบลผู้มีผลงานมากมายทั้ง CAPM Model, Sharpe Ratio และ Return Based Style Analysis
Return Based Style Analysis นั้นถือเป็นอีกหนึ่งในทฤษฎีการเงิน (Finance) ที่ออกมาเปลี่ยนโฉมหน้าการวิเคราะห์ผลการดำเนินงานของกองทุนในเวลานั้นเป็นอย่างมาก โดยก่อนหน้านี้ ขั้นตอนในการวิเคราะห์การดำเนินงานของกองทุน สามารถทำได้โดยการวิเคราะห์ข้อมูลการถือครองสินทรัพย์ที่ทางกองทุนเปิดเผยออกมารายไตรมาสหรือรายปีเท่านั้น ซึ่งในยุคนั้นแม้แต่บริษัทที่มีความเชี่ยวชาญในการทำวิจัยการลงทุนในกองทุนโดยเฉพาะอย่าง Morningstar Inc. ก็ยังมีปัญหาในการเข้าถึงข้อมูลเหล่านี้เช่นกัน
เพื่อที่จะแก้ปัญหาเหล่านี้ William F. Sharpe จึงได้นำเทคนิคการวิเคราะห์ทางสถิติที่เรียกว่า Multiple Regression ที่มักใช้ในการหาความสัมพันธ์ระหว่างตัวแปรต้นและตัวแปรตาม เข้ามาช่วยในการวิเคราะห์หาความสัมพันธ์ระหว่างผลตอบแทนของกองทุนและปัจจัย (Factor) ที่ขับเคลื่อนผลตอบแทนทั้งหลาย โดยมีจุดประสงค์ที่จะทำความเข้าใจในแนวทางการบริหารจัดการของผู้จัดการกองทุน
ซึ่งข้อมูลผลตอบแทนของกองทุนนั้นถือว่าเป็นข้อมูลสาธารณะที่นักลงทุนสามารถเข้าถึงได้ง่ายกว่าและมีการเก็บข้อมูลที่มีการปรับปรุงอย่างต่อเนื่อง (Update) มากกว่าข้อมูลรายละเอียดการถือครองสินทรัพย์เฉพาะเจาะจงของแต่ละกองทุนอยู่มาก ซึ่งการใช้ข้อมูลสาธารณะทำให้การวิเคราะห์กองทุนนั้นสามารถทำได้ง่ายขึ้นโดยไม่จำเป็นต้องเป็นนักวิเคราะห์มืออาชีพเพียงอย่างเดียว โดยใครก็ตามที่มีคอมพิวเตอร์และข้อมูลราคาของกองทุน ก็สามารถวิเคราะห์ด้วยวิธีการ Return Based Style Analysis ได้
แต่อย่างไรก็ตามผลลัพธ์จากการวิเคราะห์ Return Based Style Analysis นั้นเป็นเพียงการประมาณการเชิงสถิติเท่านั้น ซึ่ง William F. Sharpe ได้กล่าวไว้ว่า
“If it acts like a duck, assume it’s a duck.”
(ถ้ามันมีพฤติกรรมแบบเป็ด, ให้สมมุติว่ามันเป็นเป็ด)
ถ้าให้ตีความจากคำพูดของ William F. Sharpe คือ Return Based Style Analysis นั้นเป็นเพียงการวิเคราะห์จับพฤติกรรมการลงทุนผ่านผลตอบแทนของกองทุนด้วยการอนุมานเชิงสถิติ (Statistical Inference) ว่าผลตอบแทนนั้น ถูกขับเคลื่อนด้วยส่วนผสมของแต่ละปัจจัย (Factor) ในอัตราส่วนเท่าไหร่ ซึ่งจากการวิเคราะห์นั้นยังไม่อาจที่จะสรุปแบบฟันธงได้ว่า ในความเป็นจริงกองทุนมีการบริหารจัดการเป็นไปตามผลลัพธ์ของ Return Based Style Analysis โดยต้องมีการพิจารณาข้อมูลในแง่อื่นเพิ่มเติมควบคู่กันไปด้วย
คุณประโยชน์ของ Return Based Style Analysis
ในส่วนนี้เราจะมาทำความรู้จักกันถึงคุณประโยชน์หลักๆของการวิเคราะห์ด้วยเทคนิค Return Based Style Analysis ซึ่งแบ่งออกเป็นหมวดหมู่ได้ดังนี้
- ใช้ในการสร้าง Benchmark พิเศษเพื่อติดตามประสิทธิภาพในการบริหารจัดการกองทุนเมื่อเปรียบเทียบกับการลงทุนแบบ Passive
- ใช้เป็นเครื่องมือสำหรับช่วยในการจัดพอร์ตโฟลิโอการลงทุน (Asset Allocation)
- ใช้ในการติดตามกลยุทธ์การลงทุน หรือผลตอบแทนของกองทุนต่างๆ ว่ายังดำเนินกลยุทธ์เป็นไปตามปัจจัยหรือนโยบายการลงทุนที่ออกแบบมาตั้งแต่แรกหรือไม่
อย่างไรก็ตามในบทความชิ้นนี้ ผมจะขอเน้นไปที่ข้อ 3 เพียงข้อเดียวนั้นคือ ใช้สำหรับการติดตามผลลัพธ์ของกลยุทธ์การลงทุนกันครับ ซึ่งถือเป็นวัตถุประสงค์หลักของการทำ Return Based Style Analysis เลยก็ว่าได้ โดยที่การวิเคราะห์แบบ Return Based Style Analysis นั้นเป็นการนำหลักการทางสถิติมาวิเคราะห์ข้อมูลที่เกิดขึ้นในอดีต ว่าปัจจัยใดที่มีผลกระทบต่อผลตอบแทนของพอร์ตโฟลิโอบ้าง
ยกตัวอย่างเช่น เราอยากทราบว่ากองทุนที่มีนโยบายการลงทุนในหุ้นขนาดเล็กที่มีการเติบโตสูงนั้น ได้ทำตามนโยบายการลงทุนที่ให้ไว้หรือไม่? เราก็สามารถนำผลตอบแทนที่เกิดขึ้นจริงของกองทุนดังกล่าว มาทำการวิเคราะห์ด้วย Return Based Style Analysis ซึ่งผลลัพธ์ที่ได้จากการทำ จะบ่งบอกว่าผลลัพธ์ที่เกิดขึ้นนั้น เกิดขึ้นจากปัจจัยหุ้นขนาดเล็ก (Small Cap) และหุ้นเติบโต (Growth Stock) จริงหรือไม่?
อย่างไรก็ตาม ข้อจำกัดของ Return Based Style Analysis คือ เราไม่อาจที่จะใช้ทดแทนการวิเคราะห์ข้อมูลการถือครองสินทรัพย์แบบเดิมได้ทั้งหมด ซึ่งจริงๆแล้วผู้วิเคราะห์ควรนำข้อมูลที่ได้จากทั้ง 2 วิธีมาใช้วิเคราะห์ร่วมกันเพื่อปิดจุดอ่อนซึ่งกันและกันมากกว่าครับ
รู้จักกับ Multiple Regression
ในช่วงนี้ผมจะขออธิบายถึงที่มาและสูตรคณิตศาสตร์ที่เกี่ยวข้องกับการวิเคราะห์ Return Based Style Analysis กันซักนิด โดยเราจะอธิบายแบบเน้นไปที่ความเข้าใจเชิงตรรกะมากกว่าที่จะลงลึกไปในเชิงสถิติ แต่ถ้าผู้อ่านคนไหนสนใจรายละเอียดในเชิงลึกก็สามารถอ่านเพิ่มเติมได้ในส่วนอ้างอิง (Reference) ที่ท้ายบทความครับ
อย่างที่ได้กล่าวไปข้างต้นแล้วว่า Return Based Style Analysis นั้นเป็นการวิเคราะห์ด้วยวิธีการทางสถิติที่นำผลตอบแทนของกองทุน (Fund Performance) มาทำการหาความสัมพันธ์เทียบกับผลตอบแทนรวมของพอร์ตโฟลิโอที่จำลองผลตอบแทนของแต่ละปัจจัย (Passive Factor Index) ซึ่งแนวคิดนี้เริ่มมาจากสูตรผลตอบแทนของการลงทุนในทางทฤษฎีหรือ Assets Class Factor Model ดังนี้
![]()
ซึ่ง R = ผลตอบแทนของการลงทุน (Asset Return)
F = ผลตอบแทนของแต่ละปัจจัยที่ 1,2 ถึง n (Factor Return)
b = Sensitivity หรือ “น้ำหนัก” ของแต่ละปัจจัยที่ 1,2 ถึง n รวมกัน = 1 (Factor Weight)
e = ผลตอบแทนส่วนเกินที่ไม่ได้มาจากปัจจัยใดๆ (non-Factor Return)
ภาพที่ 2 : สูตร Assets Class Factor Model
ซึ่งถ้าให้อธิบายแบบง่ายๆคือ ผลตอบแทน (R) ที่เราได้รับจากการลงทุนนั้นเราจะเท่ากับ ผลรวมของผลตอบแทนจากการลงทุนในแต่ละปัจจัย (F) โดยในแต่ปัจจัยนั้น ต่างก็มีผลกระทบต่อผลตอบแทน (R) ที่ไม่เท่ากันตามค่าน้ำหนัก (b) และบวกผลรวมของทุกปัจจัยทั้งหมดกับผลตอบแทนส่วนที่ไม่ได้มาจากปัจจัยใดๆ (e) โดยจะสังเกตได้ว่าสูตร Assets Class Factor Model จริงๆแล้วก็คือ สมการ Mulitple Linear Regression ที่เรารู้จักกันนั่นเอง
![]()
ภาพที่ 3 : สูตร Assets Class Factor ที่จัดเรียงใหม่
และถ้าเราทำการจัดเรียงสมการใหม่ในรูปแบบนี้เราจะสามารถใช้เทคนิคทางคณิตศาสตร์ที่เรียกว่า Quadratic Programming Algorithm** เพื่อใช้แก้สมการที่จะหาค่าความสัมพันธ์ของค่า “น้ำหนัก” (b) ของแต่ละปัจจัย (F) ที่ทำให้ผลตอบแทนที่ไม่ได้มาจากปัจจัยใด(e) นั้นมีค่าต่ำที่สุด (Optimize for Minimum e) โดย ”น้ำหนัก” (b) ของแต่ละปัจจัยนั้นต้องมีผลรวมเท่ากับ 100% และไม่สามารถเป็นค่าติดลบได้
โดยผลที่ได้จากการแก้สมการนั้นจะออกมาเป็นสมการเชิงเส้น ที่ผลรวมของผลตอบแทนของแต่ละปัจจัย (Factor) นั้นที่มีความใกล้เคียง (Fit) กับชุดข้อมูลผลตอบแทนของกองทุนที่ต้องการวิเคราะห์มากที่สุดครับ
หมายเหตุที่ 1 : Quadratic Programming Algorithm คือวีธีการทางคณิตศาสตร์ในการแก้ปัญหา Optimization Problem ในสมการ Quadratic Function โดยสามารถอ่านข้อมูลเพิ่มเติมได้ที่นี่
รู้จักกับค่า R-Squared กันซักนิด
โดยภายหลังจากที่เราเข้าใจ Concept ของ Multiple Regression ในเบื้องต้นเป็นที่เรียบร้อยแล้ว คำถามถัดมาก็คือ เราทราบได้อย่างไรว่าปัจจัยที่เราเลือกมานั้นสามารถอธิบายผลตอบแทนได้มากน้อยเพียงใด? ซึ่งในส่วนนี้เราสามารถวัดได้ด้วยค่า R-Squared หรือเรียกได้อีกอย่างว่า Coefficient of Determination ซึ่งคำนวนมาจากสูตรดังนี้
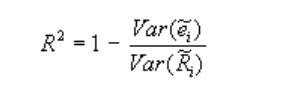
R-Squared = Coefficient of Determination
Var(e) = ค่าความแปรปรวน (Variance) ของ ผลตอบแทนส่วนเกินที่ไม่สามารถอธิบายด้วยปัจจัยใดๆ
Var(R) = ค่าความแปรปรวน (Variance) ของ ผลตอบแทนทั้งหมด
โดยค่า R-Squared นั้นจะอยู่ระหว่าง 0 – 100% :
0% คือสมการเส้นตรงที่ได้นั้นไม่สามารถอธิบายความผันแปรของผลตอบแทนการลงทุน Ri ได้เลย
100 % คือสมการเส้นตรงที่ได้นั้นสามารถอธิบายความผันแปรของผลตอบแทนการลงทุน Ri ได้ทั้งหมด
ภาพที่ 4 : สูตรการคำนวนค่า R-Squared หรือ Coefficient of Determination
หรือถ้าให้พูดง่ายๆคือ ถ้าผลลัพธ์มีค่า R-Squared ที่สูงหมายความว่าค่าน้ำหนักของแต่ละปัจจัย ที่เราได้จากการแก้สมการ Multiple Regression ในภาพที่ 2 นั้นสามารถอธิบายผลตอบแทนของการลงทุนได้มากขึ้นนั่นเอง
การประยุกต์ใช้ Return Based Style Analysis ในการวิเคราะห์กลยุทธ์การลงทุน
ในช่วงต่อไปของบทความนี้เราจะมาทำการสาธิตการนำ Return Based Style Analysis มาใช้ในการวิเคราะห์ปัจจัยที่ขับเคลื่อนผลตอบแทนของกลยุทธ์การลงทุน เพื่อที่จะทำให้เราเข้าใจพฤติกรรมผลตอบแทนของกลยุทธ์การลงทุนในช่วงระยะเวลาต่างๆได้ดียิ่งขึ้น
โดยในขั้นตอนแรกนั้น เราจำเป็นต้องทำการสร้างดัชนีอ้างอิงปัจจัยหรือ “Style” ต่างๆในของกลยุทธ์การลงทุนขึ้นมา โดยในการทดลองนี้เราจะสร้างดัชนีขึ้นมาอ้างอิง 5 ปัจจัยด้วยกันนั่นก็คือ ปัจจัยหุ้นขนาดใหญ่ (Large Cap), ปัจจัยหุ้นขนาดเล็ก (Small Cap), ปัจจัยด้านแนวโน้มของราคา (Momentum), ปัจจัยเชิงคุณค่า (Value) และปัจจัยการถือครองเงินสด (Cash)
อย่างไรก็ตาม ในส่วนนี้ผู้วิเคราะห์สามารถเพิ่มหรือลดจำนวนของดัชนีอ้างอิงขึ้นอยู่กับขอบเขตของสินทรัพย์หรือ Universe ของกลยุทธ์การลงทุน หรือกองทุนที่ต้องการทำการวิเคราะห์ ยกตัวอย่างเช่น ถ้ากลยุทธ์การลงทุนหรือกองทุนมีการลงทุนในสินค้าโภคภัณฑ์เช่น ทองคำ หรือ น้ำมัน เราก็จำเป็นต้องมีดัชนีไว้อ้างอิงผลตอบแทนของสินค้าโภคภัณฑ์เหล่านั้นเช่นกัน
ปัจจัยหุ้นขนาดใหญ่ (Large Cap Factor)
ดัชนีอ้างอิงผลตอบแทนของหุ้นขนาดใหญ่ (LargeCap) นั้นสร้างขึ้นมาจากผลตอบแทนของดัชนี SET50 ซึ่งเป็นตัวแทนของหุ้นขนาดใหญ่
ปัจจัยหุ้นขนาดเล็ก (Small Cap Factor)
ดัชนีอ้างอิงผลตอบแทนของหุ้นขนาดเล็ก (SmallCap) นั้นสร้างขึ้นมาจากผลตอบแทนของดัชนี MAI ซึ่งเป็นตัวแทนของหุ้นขนาดเล็ก
ปัจจัยด้านแนวโน้มของราคา (Momentum Factor)
ในการทดลองนี้ ดัชนีอ้างอิงปัจจัยด้านแนวโน้มของราคา (Momentum) สร้างมาจากผลตอบแทนของพอร์ตโฟลิโอที่ลงทุนในหุ้นที่มีอัตราการเปลี่ยนแปลงของราคาสูงในช่วง 6 เดือนย้อนหลังสูงที่สุด โดยจะมีการปรับพอร์ตโฟลิโอทุกๆ 6 เดือนโดยกลยุทธ์การลงทุนนี้อ้างอิงมาจากงานวิจัยของ Jegadeesh และ Titman (1993) โดยมีรายละเอียดของการสร้างดัชนีปัจจัยอ้างอิง ดังนี้
| Condition | Details |
| Backtesting Window ในการวิจัย |
|
| Backtesting Restriction |
|
| Universe |
|
| Filters |
|
| Entry |
|
| Exit |
|
| Position Size |
|
| Position Score |
|
| Order Management |
|
ตารางที่ 1 : เงื่อนไขต่างๆสำหรับการสร้างพอร์ตโฟลิโออ้างอิงปัจจัย Momentum Factor
ปัจจัยเชิงคุณค่า (Value Factor)
ส่วนดัชนีอ้างอิงปัจจัยเชิงคุณค่า (Value) นั้นจะสร้างมาจากผลตอบแทนของพอร์ตโฟลิโอที่ลงทุนในหุ้นที่มี P/BV ต่ำที่สุด โดยจะมีการปรับพอร์ตโฟลิโอทุกๆ 1 ปี ซึ่งกลยุทธ์การลงทุนนี้อ้างอิงมาจากงานวิจัยของ Eugene F. Fama และ Kenneth R. French (2014) โดยมีรายละเอียดของการสร้างดัชนีปัจจัยอ้างอิงดังนี้
| Condition | Details |
| Backtesting Window |
|
| Backtesting Restriction |
|
| Universe |
|
| Filters |
|
| Entry |
|
| Exit |
|
| Position Size |
|
| Position Score |
|
| Order Management |
|
ตารางที่ 2 : เงื่อนไขต่างๆสำหรับการสร้างพอร์ตโฟลิโออ้างอิงปัจจัย Value Factor
ปัจจัยเงินสด (Cash Factor)
ดัชนีอ้างอิงดอกเบี้ยเงินฝากนั้นถูกสร้างขึ้นมาเพื่อที่จะจำลองผลตอบแทนของระบบจากการถือครองเงินสดโดย ในการทดสอบครั้งนี้เราจะใช้อัตราดอกเบี้ยเงินฝากคงที่ 2% ต่อปีซึ่งเป็นค่าเฉลี่ย 20 ปีของดอกเบี้ยเงินฝากของประเทศไทย
และเมื่อเราได้ดัชนีอ้างอิงปัจจัยต่างๆในการทำนายผลตอบแทนเหล่านี้แล้ว สิ่งที่เรายังขาดอยู่ก็คือ เราจะวิเคราะห์ผลตอบแทนของอะไร ซึ่งจะพูดถึงในส่วนถัดไปนี้
หมายเหตุที่ 2 : สิ่งสำคัญที่เป็นหัวใจของการวิเคราะห์ Return Based Style Analysis คือ การเลือกใช้หรือสร้างดัชนีที่จะอ้างอิงผลตอบแทนของแต่ละปัจจัย (Factor) นั้นต้องสามารถอธิบายได้ (Comprehensive) และถ้าเป็นไปได้ต้องไม่มีการทับซ้อนกัน (Mutually Exclusive) เพราะถ้าดัชนีอ้างอิงของแต่ละปัจจัยนั้นมีความใกล้เคียงกันหรือมีการทับซ้อนกันมากจนเกินไปจะส่งผลให้ผลลัพธ์ที่ออกมาจากการวิเคราะห์นั้นไม่มีความเสถียร (มีการกระโดดกลับไปมาระหว่าง 2 ปัจจัย) และไม่สามารถเชื่อถือได้
กลยุทธ์ที่ต้องการวิเคราะห์ (Input System)
กลยุทธ์การลงทุนที่เราจะนำมาวิเคราะห์เป็นตัวอย่างคือกลยุทธ์การลงทุน Mangmao ATH จากชุดโค้ดและฐานข้อมูล The Alpha Suite โดยสามารถอ่านรายละเอียดของแนวคิดและเงื่อนไขของกลยุทธ์การลงทุนนี้ได้ในหนังสือแมงเม่าคลับ โดยมีรายละเอียดของการทดสอบโดยย่อดังนี้
หมายเหตุที่ 3 : การทดสอบนี้เราจะไม่ใส่ค่า Slippage เข้าไปเนื่องจากผลกระทบของค่า Slippage นั้นอาจไปกระทบผลจากการวิเคราะห์ด้วย Return Based Style Analysis
| Condition | Details |
| Backtesting Window |
|
| Backtesting Restriction |
|
| Universe |
|
| Filters |
|
| Entry |
|
| Exit |
|
| Position Size |
|
| Position Score |
|
| Order Management |
|
ตารางที่ 3 : เงื่อนไขสำหรับการทดสอบกลยุทธ์การลงทุน Mangmao ATH
สิ่งที่คิดกับสิ่งที่เป็นอาจไม่ใช่สิ่งเดียวกัน !!
ผลลัพธ์ที่ออกมาจากการวิเคราะห์ข้อมูลผลตอบแทนย้อนหลังด้วย Return Based Style Analysis นั้นถือว่ามีความน่าสนใจเป็นอย่างมาก เนื่องจากผลลัพธ์ที่แสดงปัจจัยที่ขับเคลื่อนผลตอบแทนของกลยุทธ์ ที่เราเข้าใจว่าเป็นแก่นของระบบลงทุนนั้นกลับไม่ได้เป็นสิ่งเดียวกับที่เราคิด โดยก่อนอื่นเราจะมาดูภาพ Cummulative Return และค่าสถิติจากการทดสอบวิจัยย้อนหลัง (Backtest) ของระบบ Mangmao ATH และดัชนีตัวแทนปัจจัยขับเคลื่อนต่างๆ (Factors) ในภาพที่ 5 และตารางที่ 4 ด้านล่าง

ภาพที่ 5 : Cumulative Return แบบรายเดือนของกลยุทธ์การลงทุน Mangmao ATH (เขียว) เปรียบเทียบกับดัชนีตัวแทนปัจจัยขับเคลื่อนต่างๆ (Factors) ตั้งแต่ปี 2003 ถึงปลายปี 2018
| Portfolio Metrics | Mangmao ATH | LargeCap | SmallCap | Momentum | Value |
| Cumulative Profit | 24.88 | 3.36 | 1.90 | 10.93 | 13.74 |
| Annualized Return % (CAGR) | 22.68 | 9.69 | 6.91 | 16.86 | 18.42 |
| Ann. Standard Deviation % | 18.35 | 21.11 | 25.82 | 27.96 | 21.59 |
| Annualized Sharpe (Rf = 4%) | 1.21 | 0.44 | 0.25 | 0.59 | 0.84 |
| Max DD % | -19.45 | -58.41 | -61.80 | -60.75 | -40.08 |
| Longest DD (Months) | 25m | 35m | 109m | 48m | 29m |
| Correlation with SET Index | 0.5407 | 0.9842 | 0.6361 | 0.7044 | 0.7094 |
ตารางที่ 4 : สรุปค่าสถิติของกลยุทธ์การลงทุน Mangmao ATH เปรียบเทียบกับดัชนีตัวแทนปัจจัยขับเคลื่อนต่างๆ (Factors) ตั้งแต่ปี 2003 ถึงปลายปี 2018
ถ้าสังเกตด้วยตาเปล่าจะเห็นว่าเส้น Equity ของระบบลงทุน Mangmao ATH นั้นมีช่วงเวลาที่เคลื่อนไหวใกล้เคียงกับดัชนีตัวแทนปัจจัยทั้ง 4 แต่ก็มีในบางช่วงที่ระบบ Mangmao ATH นั้นไม่ได้เคลื่อนไหวไปในทิศทางเดียวกับปัจจัยเหล่านี้ ซึ่งการวิเคราะห์ Return Based Style Analysis นั้นจะช่วยทำให้เราเห็นถึงรายละเอียดของความสัมพันธ์ของการเคลื่อนไหวนี้ในเชิงตัวเลข โดยเป็นค่าเฉลี่ยของทั้งช่วงเวลา โดยจะได้ผลลัพธ์ดังนี้
อธิบายผลตอบแทนของกลยุทธ์ Mangmao ATH ด้วย Return Based Style Analysis
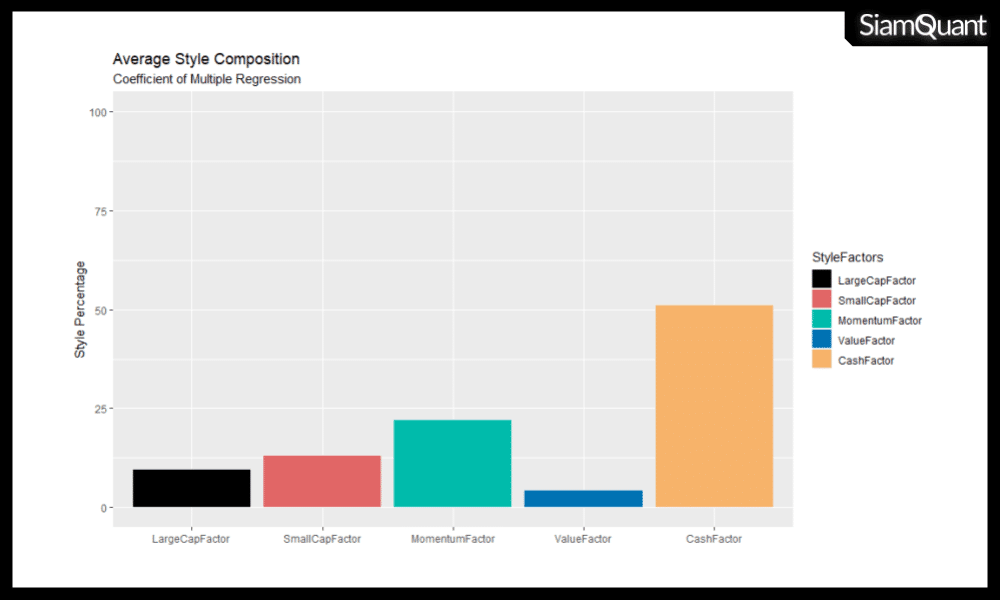
ภาพที่ 6 : แสดงค่าน้ำหนักเฉลี่ยของแต่ละปัจจัยที่เป็นตัวขับเคลื่อนผลตอบแทนของกลยุทธ์การลงทุน Mangmao ATH ในช่วงเวลาทดสอบ (ตั้งแต่ปี 2003 ถึงปลายปี 2018)
จากผลลัพธ์ข้างต้นที่ออกมานั้น เราสามารถตีความได้ว่าแท้จริงแล้วผลตอบแทนของกลยุทธ์ Mangmao ATH ซึ่งเป็นกลยุทธ์ประเภท Momentum แต่กลับมีน้ำหนักของ Cash Factor ที่สูงถึง 51% เนื่องจากกลยุทธ์การลงทุนนั้นไม่ได้มีการถือหุ้นอยู่ในพอร์ตโฟลิโอตลอดเวลา (Buy & Hold) เหมือนกับระบบที่อ้างอิงปัจจัยอื่นๆที่มีการปรับพอร์ตโฟลิโอรายปี (Rotation) ซึ่งแสดงให้เห็นพลังของการจับจังหวะซื้อขาย (Entry/Exit Timing)
โดยประโยชน์ของการถือเงินสดคือ ช่วยลดความเสี่ยงในช่วงที่ภาวะตลาดเป็นขาลง ซึ่งเห็นได้จากค่า Maximum Drawdown ของกลยุทธ์ Mangmao ATH ที่ต่ำกว่าปัจจัยอ้างอิงทั้ง 4 อย่างมีนัยยะ
อีกข้อสังเกตที่น่าสนใจคือ จะเห็นได้ว่าถึงแม้ผลตอบแทนของกลยุทธ์จะอยู่ที่ปัจจัย Momentum (22%) เป็นหลัก แต่ก็มีส่วนที่ถูกขับเคลื่อนด้วยปัจจัย SmallCap (13%), LargeCap (9%) และ Value (4%) อยู่ด้วยเช่นกัน หมายความว่านอกจากปัจจัยด้าน Momentum แล้ว ปัจจัยด้านขนาดของหุ้นทั้งหุ้นเล็กและหุ้นใหญ่ก็มีผลด้วย โดยหุ้นขนาดเล็กจะมีสัดส่วนการขับเคลื่อนผลตอบแทนที่สูงกว่าหุ้นขนาดใหญ่
อย่างไรก็ตามการวิเคราะห์แบบค่าเฉลี่ยของทั้งช่วงเวลาการทดสอบนั้นอาจทำให้เราพลาดรายละเอียดสำคัญไปได้ ซึ่ง Rolling Return Style จะเป็นอีกเทคนิคหนึ่งที่สามารถช่วยวิเคราะห์การเปลี่ยนแปลงของค่าน้ำหนักของแต่ละปัจจัย (Factor) การลงทุนในแต่ละช่วงเวลาแบบในภาพที่ 7
ซึ่งเทคนิคนี้ถือว่ามีประโยชน์มากในกรณีที่เราต้องการวิเคราะห์เจาะลึกเข้าไปในแต่ละช่วงเวลาของกลยุทธ์การลงทุนที่ตอบสนองต่อปัจจัยต่างๆ โดยในบทความนี้เราจะเลือกใช้การคำนวนน้ำหนักของทั้ง 5 ปัจจัยในแต่ละจุดของเวลา จากข้อมูลย้อนหลัง 36 เดือนแทน (3 ปี) โดยพื้นที่แต่ละสีนั้นแสดงถึงค่าน้ำหนักของแต่ละปัจจัยโดยในแต่ละช่วงเวลา โดยค่าน้ำหนักนั้นจะรวมกันเท่ากับ 1
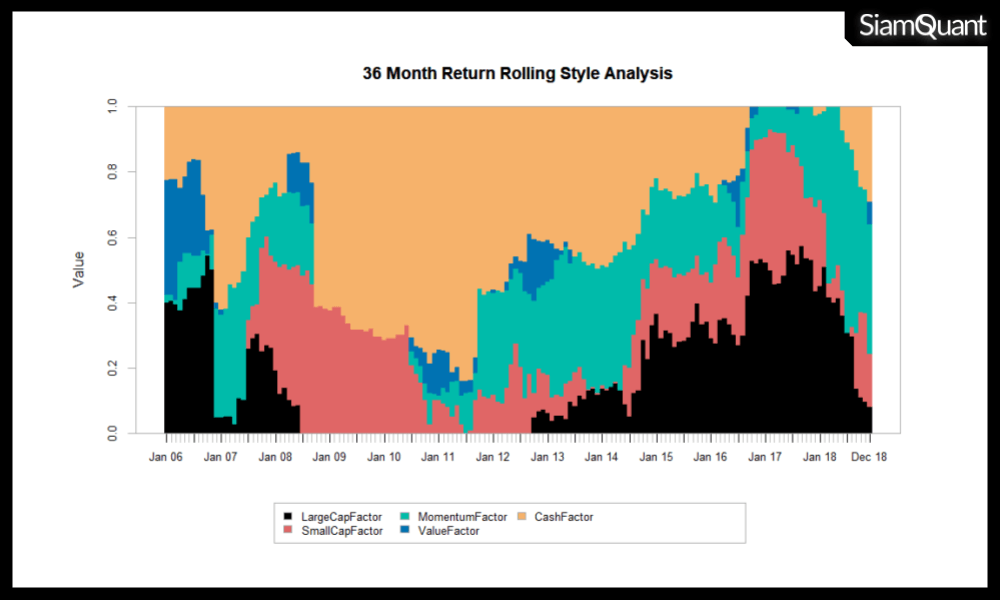
ภาพที่ 7 : Rolling Return Style Chart แสดงการเปลี่ยนแปลงน้ำหนักของแต่ละปัจจัยเฉลี่ยย้อนหลัง 36 เดือน (3 ปี)
โดยถ้าพิจารณาจาก Rolling Return Style Chart จะเห็นได้ว่าในช่วงที่ตลาดเป็นขาลงใหญ่ในช่วงปี 2008 นั้นค่า Style ของ Cash Factor นั้นพุ่งสูงขึ้นอย่างมีนัยยะ เนื่องจากกลยุทธ์ Mangmao ATH นั้นแทบที่จะไม่ได้มีการซื้อขายเลยในช่วงตลาดขาลงเกือบ 2 ปีเต็ม (สังเกตได้จากเส้น Equity ในภาพที่ 5 ที่แบนราบในช่วงปี 2008-2010) ซึ่งสอดคล้องกับผลการทดสอบก่อนหน้า
อีกจุดที่น่าตั้งข้อสังเกตคือ ถึงแม้ Bar Chart จะแสดงว่าค่าเฉลี่ยของทั้งช่วงเวลาการทดสอบ ปี 2003-2018 ของปัจจัย LargeCap จะไม่ต่างจากปัจจัย SmallCap มากนัก แต่ถ้าดูจากภาพ Rolling Return Style Chart จะเห็นรายละเอียดที่ชัดเจนยิ่งขึ้นคือ มีทั้งช่วงเวลาที่ 2 ปัจจัยนี้สลับกันมา (2006-2010) หรือมาพร้อมๆกัน (2015-2018) ซึ่งประเด็นดังกล่าวนี้นับเป็นองค์ความรู้ที่น่าไปค้นคว้าวิจัยต่อ
หมายเหตุที่ 4 : การคำนวนแบบ Rolling Style Chart 3 ปี คือการทำ Multiple Regression เพื่อแก้สมการหาน้ำหนักของแต่ละปัจจัยในแต่ละจุดข้อมูลจากข้อมูลผลตอบแทนย้อนหลัง 3 ปี
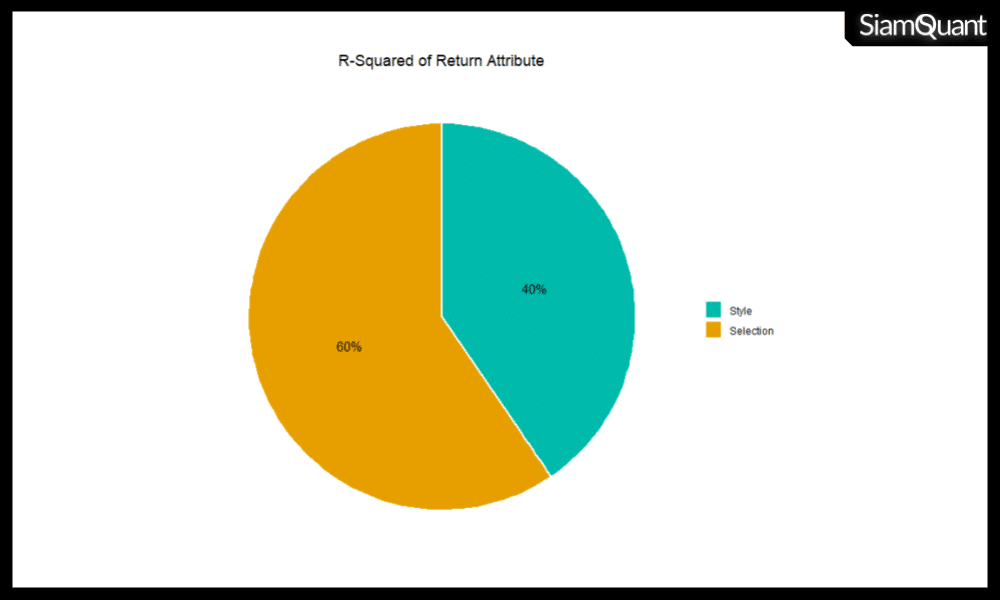
ภาพที่ 8 : ค่า R-Squared ของการวิเคราะห์กลยุทธ์การลงทุน Mangmao ATH
จากภาพที่ข้างต้น เป็นภาพแสดงอัตราส่วนของผลตอบแทนที่สามารถอธิบายได้ด้วยดัชนีของปัจจัยอ้างอิงนั้นจะเรียกว่า “Style” และส่วนไม่สามารถอธิบายได้ด้วยดัชนีของปัจจัยอ้างอิงใดๆในนั้นจะเรียกว่า “Selection” เพราะว่าที่มาของผลตอบแทนนั้นอาจเกิดขึ้นมาจากความพยายามของผู้จัดการกองทุนในการจับจังหวะซื้อขาย (Timing) หรือการเลือกลงทุนในหุ้นรายตัว (Stock Selection) ซึ่งอาจทำให้ผลตอบแทนนั้นไม่ได้มีการเคลื่อนไหวไปตามดัชนีของปัจจัยอ้างอิง (Factor Benchmark) ใดๆที่เราได้เลือกมาอ้างอิง
โดยจะเห็นได้ว่าในกรณีของกลยุทธ์ Mangmao ATH ที่เป็นกลยุทธ์จับจังหวะซื้อขายนั้นจะมีค่า R-Squared ที่ 40% หมายความว่า จากโมเดล Return Based Style Analysis ดังกล่าวเราสามารถอธิบายที่มาของผลตอบแทนได้ 40% โดยสาเหตุที่เป็นเช่นนี้อาจเกิดได้จากหลายปัจจัยด้วยกันเช่น
- ดัชนีอ้างอิงปัจจัย Momentum และ Value นั้นถูกสร้างมาจากกลยุทธ์แบบ Rotation
- ระบบ Mangmao ATH นั้นสร้างผลตอบแทนจากการจับจังหวะ (Timing) ซึ่งเป็นปัจจัยที่ไม่ได้ถูกอ้างอิงในโมเดลคณิตศาสตร์ของการทดสอบนี้
อย่างไรก็ตาม การที่ผลลัพธ์มามีค่า R-Squared ต่ำนั้นไม่ได้หมายความว่าการวิเคราะห์ล้มเหลว ซึ่งในกรณีนี้เราอาจตีความได้ว่าความสามารถในการจับจังหวะและการคัดกรองหุ้นของกลยุทธ์การลงทุน Mangmao ATH นั้นสามารถสร้างผลตอบแทนได้อย่างมีนัยยะ หรืออาจมีปัจจัยบางอย่างที่ขับเคลื่อนผลตอบแทนของระบบที่ดัชนีปัจจัยอ้างอิงนั้นไม่สามารถทดแทนได้ โดยผู้วิจัยอาจต้องมีการสร้างดัชนีปัจจัยอ้างอิงขึ้นมาเพิ่มเติม
บทสรุปของ Return Based Style Analysis
การวิเคราะห์ Return Based Style Analysis นั้นเป็นความพยายามของนักวิชาการที่จะเข้าใจพฤติกรรมของกลยุทธ์การลงทุน โดยการนำข้อมูลผลตอบแทนของปัจจัยต่างๆมาอธิบาย ด้วยกระบวนการเทคนิคทางสถิติ แทนที่จะต้องทำกระบวนการวิเคราะห์ข้อมูลการถือครองสินทรัพย์ของแต่ละกองทุนซึ่งจะทำให้ต้องใช้ทรัพยากรเป็นจำนวนมาก
ซึ่งถ้ามองในมุมมองของผู้ออกแบบกลยุทธ์การลงทุน การวิเคราะห์ Return Based Style Analysis นั้นสามารถเป็นเครื่องมือที่ช่วยให้เราเข้าใจพฤติกรรมของกลยุทธ์การลงทุนได้อย่างลึกซึ่งยิ่งขึ้น เพราะการที่เราเข้าใจถึงหลักการทำงานของกลยุทธ์นั้นๆ ทำให้เราสามารถสร้างดัชนีตัวแทนของปัจจัยต่างๆขึ้นมาอธิบายผลตอบแทนได้อย่างแม่นยำมากขึ้น
ซึ่งจะเป็นประโยชน์อย่างมากในการติดตามผลการลงทุนทั้งในการทดสอบย้อนหลังและซื้อขายจริง โดยสามารถใช้ในการสื่อสารให้นักลงทุนได้เข้าใจถึงกลยุทธ์การลงทุนและปัจจัยที่มีผลกระทบต่อผลตอบแทนของกลยุทธ์การลงทุนในช่วงเวลาต่างๆมากขึ้นครับ
แต่ในกรณีการวิเคราะห์ปัจจัยขับเคลื่อนของกองทุนที่เราลงทุนนั้น ต้องอย่าลืมว่าเราจำเป็นต้องใช้การวิเคราะห์ข้อมูลการถือครองสินทรัพย์แบบเฉพาะเจาะจงของแต่ละกองทุนควบคู่กันไปด้วย เพื่อเป็นการวิเคราะห์อย่างรอบด้านก่อนจะสรุปผลนะครับ
หมายเหตุที่ 5 : การวิเคราะห์นโยบายการลงทุนของแต่ละกองทุนนั้นด้วย Return Based Style Analysis ในประเทศไทยนั้นยังมีข้อจำกัดในหลายๆด้าน ทั้งเรื่องของข้อมูลที่ใช้ในการสร้างปัจจัยอ้างอิงนั้นยังมีอยู่น้อยเมื่อเทียบกับตลาดต่างประเทศ, การสร้างปัจจัยอ้างอิงที่เหมาะสม และผู้วิเคราะห์เองต้องมีทั้งประสบการณ์การลงทุนที่มากพอเพื่อที่จะตีความผลลัพธ์จากการวิเคราะห์ได้อย่างสมเหตุสมผล
References :
Asset Allocation : Management Style and Performance Measurement ; William F. Sharpe https://web.stanford.edu/~wfsharpe/art/sa/sa.htm
The Role of Returns-Based Style Analysis: Understanding, Implementing, and Interpreting the Technique; Lori Lucas, CFA and Mark W. Riepe, CFA https://corporate.morningstar.com/ib/documents/MethodologyDocuments/IBBAssociates/ReturnsBasedAnalysis.pdf
Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency Narasimhan Jegadeesh and Sheridan Titman
https://www.jstor.org/stable/2328882?seq=1#page_scan_tab_contents
A Five-Factor Asset Pricing Model ; Eugene F. Fama and Kenneth R. French https://www8.gsb.columbia.edu/programs/sites/programs/files/finance/Finance%20Seminar/spring%202014/ken%20french.pdf