Overfitting bias ปัญหาอันน่าหนักใจของควอนท์
อันตรายอย่างหนึ่งของการเป็นควอนท์ก็คือ การที่เราค้นพบกลยุทธ์บางอย่างที่สามารถทำกำไรได้ดีในอดีต และนำมันไปใช้โดยคิดว่าจะสามารถทำกำไรได้เช่นเดียวกันในอนาคต ทั้งที่ความจริงแล้วกลยุทธ์ดังกล่าวอาจทำกำไรได้เพียงเพราะความ “โชคดี” เท่านั้น
ควอนท์ที่ดีจะมีเครื่องมือที่ใช้ตรวจสอบสิ่งเหล่านี้ แน่นอนว่าวิธีที่ดีที่สุดคือการทดสอบกลยุทธ์ดังกล่าวกับข้อมูลนอกกลุ่มตัวอย่าง (Out-of-sample test) แต่หากเราไม่มีข้อมูลดังกล่าวแล้วล่ะก็ เราอาจจะต้องพึ่งพาผลการทดสอบกับข้อมูลในกลุ่มตัวอย่าง (In-sample test) เป็นหลัก โดยเราจะมองหากลยุทธ์ที่สามารถทำกำไรได้มากกว่าตัวชี้วัด (Benchmark) อย่างมีนัยสำคัญทางสถิติ ซึ่งการทดสอบที่เรานิยมใช้อย่างหนึ่งคือ t-test
ใน t-test นั้นเราจะคำนวณสิ่งที่เรียกว่าค่า t-value ของกลยุทธ์ที่ทำการทดสอบออกมา และทำการเปรียบเทียบกับเกณฑ์ซึ่งมีชื่อเรียกว่าค่าวิกฤต (Critical value of t) หากค่า t-value ของกลยุทธ์มีค่ามากกว่าค่าวิกฤตดังกล่าวจะถือว่ากลยุทธ์สามารถทำกำไรได้มากกว่าตัวชี้วัดอย่างมีนัยสำคัญทางสถิติ หรือพูดอีกนัยหนึ่งก็คือกลยุทธ์มีความสามารถในการทำกำไรที่แท้จริง (ไม่ได้เกิดจากความบังเอิญหรือโชคดี) นั่นเอง
Robert Novy-Marx ศาสตราจารย์แห่งมหาวิทยาลัยโรเชสเตอร์
รูปที่ 1 : ศาสตราจารย์ Robert Novy-Marx
โดยปกติแล้วค่าวิกฤตที่เรานิยมใช้กันคือ 1.96 (two-tailed test, alpha = 0.05) แต่ Novy-Marx ได้โต้แย้งว่าหากกลยุทธ์ที่ทำการทดสอบนั้นประกอบไปด้วยกฏเกณฑ์การซื้อขายเป็นจำนวนมาก กลยุทธ์เหล่านั้นจะได้รับผลกระทบจากสิ่งที่เรียกว่า Overfitting bias ซึ่งส่งผลให้ค่า t-value ที่คำนวณได้สูงกว่าปกติ หากเรายังใช้ค่าวิกฤตเดิมเป็นเกณฑ์จะทำให้ผลการทดสอบกลยุทธ์ดังกล่าวมีโอกาสเกิดนัยสำคัญทางสถิติได้มากกว่ากลยุทธ์ทั่วไป
ด้วยเหตุนี้เอง Novy-Marx จึงได้ทำการศึกษาเพื่อหาค่าวิกฤตที่เหมาะสมกับการทดสอบกลยุทธ์ที่มีกฏเกณฑ์การซื้อขายจำนวนมาก โดยในงานวิจัยของเขา(1) ได้ยกตัวอย่างถึงกลยุทธ์ที่มีลักษณะดังกล่าวไว้เช่น
- Piotroski’s F-score (2000)
ประเมินความแข็งแกร่งทางการเงินจากกฏ 9 ข้อ
- Gompers, Ishii, and Metrick’s Governance Index (2003)
ประเมินสิทธิของผู้ถือหุ้นจากกฏ 24 ข้อ
- Baker and Wurgler Sentiment Index (2006)
ประเมินความเชื่อมั่นนักลงทุนจากกฏ 6 ข้อ
- Asness, Frazzini, and Pedersen’s Quality score (2013)
ประเมินคุณภาพของหุ้นเติบโตจากกฏ 21 ข้อ
- Stambaugh and Yuan’s Mispricing factors (2015)
ประเมินราคาที่บิดเบือนจากกฏ 11 ข้อ
เขาได้ตั้งข้อสังเกตว่าในกระบวนการวิจัยและพัฒนากลยุทธ์เหล่านี้ นักวิจัยมักจะทดสอบกฏเกณฑ์การซื้อขายจำนวนมากกับข้อมูลในอดีต จากนั้นทำการ Optimize เพื่อให้ได้การผสมกันของกฏที่มีผลการทดสอบดีที่สุด โดยส่วนใหญ่มักจะเกิดขึ้นใน 2 รูปแบบคือ
1. Equal-weighted: กำหนดให้กฏแต่ละข้อมีค่าน้ำหนักเท่ากัน ยกตัวอย่างเช่น F-score, Governance Index เป็นต้น
2. Signal-weighted: กำหนดให้กฏแต่ละข้อมีค่าน้ำหนักต่างกัน ยกตัวอย่างเช่น Sentiment Index, Quality score, Mispricing factors เป็นต้น
การกระทำเหล่านี้ล้วนทำให้เกิด Overfitting bias กับกลยุทธ์ ซึ่งส่งผลต่อการคำนวณค่า t-value ดังที่ได้กล่าวไปแล้ว
งานวิจัยของ Robert Novy-Marx
เพื่อหาค่าวิกฤตที่เหมาะสมในการทดสอบกลยุทธ์ที่ได้รับผลกระทบจาก Overfitting bias ดังกล่าว Novy-Marx ได้กระทำดังต่อไปนี้
1. สร้างกฏเกณฑ์การซื้อขายแบบสุ่มจำนวนมากขึ้นมา ซึ่งกฏเหล่านี้ไม่มีความสามารถในการทำกำไรที่แท้จริงใดๆ
2. นำข้อมูลตลาดหุ้นสหรัฐจำนวน 20 ปี ตั้งแต่เดือนมกราคม ปี 1995 จนถึงเดือนธันวาคมปี 2014 มาเพื่อหาผลตอบแทนจากการใช้กฏดังกล่าวในรูปแบบต่างๆคือ
· การเลือกใช้กฏที่ดีที่สุดเพียงกฏเดียว (Single best signal)
· การผสมกฏแบบ Equal-weighted
· การผสมกฏแบบ Signal-weighted
3. ใช้ข้อมูลผลตอบแทนเหล่านั้น ทำการคำนวณหาค่าวิกฤตที่เหมาะสมในแต่ละกรณีขึ้นใหม่ ซึ่งได้แสดงผลการคำนวณไว้ในรูปที่ 2 (ผู้ที่สนใจในวิธีการคำนวณโดยละเอียดสามารถเข้าไปศึกษาเพิ่มเติมได้ในงานวิจัยของเขา(1))
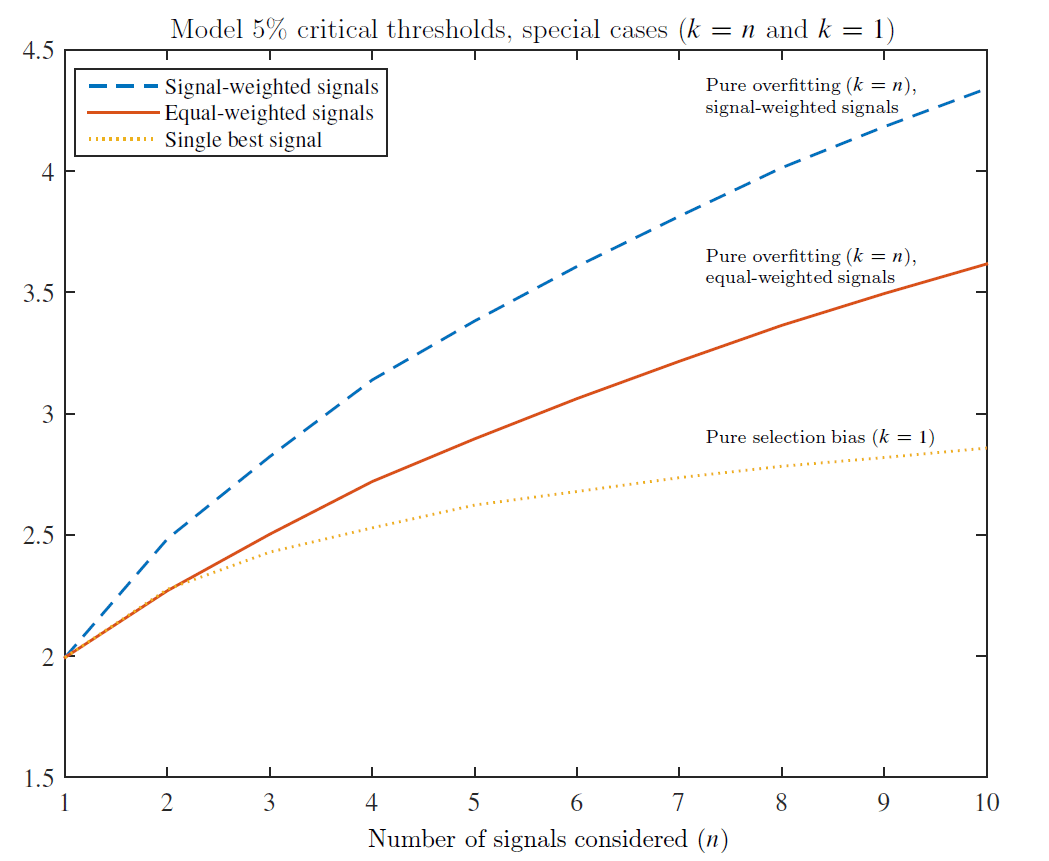
รูปที่ 2 : กราฟแสดงค่าวิกฤตที่เหมาะสม (two-tailed test, alpha = 0.05)
สิ่งที่เราสังเกตได้จากกราฟมีดังต่อไปนี้
- หากกลยุทธ์มีกฏเกณฑ์การซื้อขายเพียงกฏเดียว ค่าวิกฤตที่เหมาะสมยังคงเป็น 1.96 เช่นเดิม
- สำหรับกลยุทธ์ที่ใช้วิธี Equal-weighted (เส้นทึบสีแดง) ยิ่งจำนวนกฏเกณฑ์การซื้อขายมีมากขึ้นเท่าไหร่ ผลของ Overfitting bias ที่มีต่อกลยุทธ์ก็จะยิ่งมากขึ้นเท่านั้น ด้วยเหตุนี้ค่าวิกฤตที่เหมาะสมจึงแปรผันตามจำนวนกฏนั่นเอง
- สำหรับกลยุทธ์ที่ใช้วิธี Signal-weighted (เส้นประสีน้ำเงิน) ค่าวิกฤตที่เหมาะสมจะแปรผันตามจำนวนกฏเช่นเดียวกัน แต่สังเกตว่าหากจำนวนกฏเท่ากันค่าวิกฤตที่เหมาะสมของ Signal-weighted จะสูงกว่า Equal-weighted มาก ซึ่งแสดงให้เห็นว่ากลยุทธ์ที่ใช้ Signal-weighted นั้นได้รับผลกระทบจาก Overfitting bias มากกว่า
คำแนะนำสำหรับกลยุทธ์ที่มีกฏเกณฑ์การซื้อขายจำนวนมาก
โดยสรุป Novy-Marx ไม่ได้บอกว่ากลยุทธ์ที่มีกฏเกณฑ์การซื้อขายจำนวนมากนั้นใช้ไม่ได้ แต่ต้องการเน้นย้ำว่าการทดสอบทางสถิติสำหรับกลยุทธ์เหล่านั้นต้องกระทำต่างจากกลยุทธ์ทั่วไป ทั้งนี้เพราะผลกระทบจาก Overfitting bias นั่นเอง ซึ่งเราสามารถสรุปคำแนะนำของเขาได้เป็น 2 กรณีดังนี้
1. ทำการทดสอบกลยุทธ์เหล่านั้นตามปกติ แต่ค่าวิกฤต (Critical value of t) ที่ใช้ต้องถูกปรับปรุง ทั้งนี้ Novy-Marx ได้แนะนำสูตรสำหรับการคำนวณค่าดังกล่าวไว้ในงานวิจัยของเขา(1) (สมการที่ 12 และ 15 สำหรับกลยุทธ์ที่มีการผสมกฏแบบ Equal-weighted และ Signal-weighted ตามลำดับครับ)
2. ทำการทดสอบกฏเกณฑ์การซื้อขายในกลยุทธ์เหล่านั้นแยกกันครั้งละ 1 กฏ โดยทำการปรับระดับนัยสำคัญทางสถิติของการทดสอบแต่ละครั้งด้วย Bonferroni correction ยกตัวอย่างเช่น หากกลยุทธ์ที่เราต้องการทดสอบมีกฏเกณฑ์การซื้อขายรวมทั้งสิ้น 10 กฏ และเราต้องการผลการทดสอบที่ระดับนัยสำคัญ 0.05 จะสามารถทำได้โดยทดสอบครั้งละ 1 กฏรวมทั้งสิ้น 10 ครั้ง โดยปรับระดับนัยสำคัญแต่ละครั้งเป็น 0.05 / 10 = 0.005 นั่นเอง
ในบทความนี้เราได้หยิบยกเพียงส่วนหนึ่งของงานวิจัยที่ Novy-Marx ทำการศึกษาไว้มาสรุปให้อ่านกัน แต่ในงานวิจัยดังกล่าวยังมีสิ่งอื่นๆที่น่าสนใจอีกมาก ยกตัวอย่างเช่น ผลของ Selection bias ต่อกลยุทธ์ที่มีกฏเกณฑ์การซื้อขายจำนวนมาก, ความสัมพันธ์ระหว่าง Overfitting bias กับ Selection bias และการคำนวณค่าวิกฤตที่เหมาะสมสำหรับกรณีอื่นๆ (Selection bias, Mix bias) เป็นต้น หากท่านใดสนใจ สามารถศึกษาเพิ่มเติมได้จากงานวิจัยฉบับเต็มตามลิงก์ที่อยู่ใน Reference ครับ
ทีมงาน SiamQuant
SiamQuant Academy จุดเริ่มต้นของการลงทุนอย่างเป็นระบบ
Reference
1. Robert Novy-Marx. ( 2016 ). Testing strategies based on multiple signals.
2. David Foulke. ( 2016 ). Backtesting strategies based on multiple signals — Beware of overfitting bias!.